rdrr

README

rdrr (version 1)

Regionally Distributed Runoff Recharge model is a large-scale high-resolution grid-based numerical model optimized for implementation on parallel computer architectures. No process of the model is in any way novel, rather a suite of existing model structures have been combined into one platform chosen specifically for their ease of implementation and computational scalability.

The model's primary intention is to interpolate watershed moisture conditions for the purposes of estimating regional groundwater recharge, given all available data. While the model can project stream flow discharge and overland runoff at any point in space, the model is not optimized, nor intended to serve as your typical rainfall runoff model. Outputs from this model will most often be used to constrain regional groundwater models withing the Oak Ridges Moraine Groundwater Program (ORMGP) jurisdiction in southern Ontario, Canada.

This model is currently in beta mode, and its use for practical application should proceed with caution. Users should be aware that results posted online are subject to change. Ultimately, the intent of this model is to produced ranges of long-term (monthly and greater) water budgeting as a hydrological reference for the partners of the ORMGP.

TOPMODEL

The groundwater model structure employed here follows the TOPMODEL structure of Beven and Kirkby (1979). TOPMODEL employs a distribution function that projects predicted groundwater discharge at surface from a simple groundwater storage reservoir. The distribution function is referred to as the "soil-topologic index" (Beven, 1986) which factors distributed surficial material properties, land surface gradients, and upslope contributing areas. TOPMODEL does not explicitly model integrated groundwater/surface water processes, however it does provide the ability, albeit an indirect one, to include the influence of near-surface watertables. Most importantly, low-lying areas close to drainage features will be prevented from accepting recharge resulting in saturated overland flow conditions.

Assumptions to TOPMODEL are that the groundwater reservoir is lumped meaning it is equivalently and instantaneously connected over its entire spatial extent. This assumption implies that recharge computed to a groundwater reservoir is uniformly applied to its water table. The groundwater reservoir is thought to be a shallow, single-layered, unconfined aquifer whose hydraulic gradient can be approximated by local surface slope.

Lateral (downslope) transmissivity $(T)$ is then assumed to scale exponentially with soil moisture deficit $(D)$ by:

$$ T = T_o\exp{\left(\frac{-D}{m}\right)}, % T = T_o\exp{\left(\frac{-D}{m}\right)} = T_o\exp{\left(\frac{-\phi z_\text{wt}}{m}\right)}, $$

where $T_o=wK_\text{sat}$ is the saturated lateral transmissivity perpendicular to an iso-potential contour of unit length $(w)$ [m²/s] that occurs when no soil moisture deficit exists (i.e., $D=0$) and $m$ is a scaling factor [m]. Consequently, recharge computed in the distributed sense is aggregated when added to the lumped reservoir, yet discharge to surface remains distributed according to the soil-topographic index and stream location. For additional discussion on theory and assumptions, please refer to Beven et.al., (1995), Ambroise et.al., (1996) and Beven (2012).

Under the assumption that the groundwater reservoir is unconfined lends the model the ability to predict the depth to the water table $(z_{wt})$ when porosity $(\phi)$ is known and $D>0$:

$$ D=\phi z_{wt} $$

At the regional scale, multiple TOPMODEL reservoirs have been established to represent groundwater dynamics in greater physiographic regions, where it is assumed that material properties are functionally similar and groundwater dynamics are locally in sync. Groundwater discharge estimates from each TOPMODEL reservoir instantaneously contributes lateral discharge to stream channel cells according to Darcy's law:

$$ q = T\tan\beta, $$

where $q$ is interpreted here as groundwater discharge per unit length of stream/iso-potential contour [m²/s], and $\tan\beta$ is the surface slope angle in the downslope direction, assumed representative of the saturated zone's hydraulic gradient.

The sub-surface storage deficit $(D_i)$ at grid cell $i$ is determined using the distribution function:

$$ D_i = \overline{D} + m \left(\gamma - \zeta_i\right), $$

where $\zeta_i$ is the soil-topologic index at cell $i$, defined by $\zeta=\ln(a/T_o \tan \beta)$ and $a_i$ is the unit contributing area defined here as the total contributing area to cell $i$ divided by the cell's width $w$. The catchment average soil-topologic index:

$$ \gamma = \frac{1}{A}\sum_i A_i\zeta_i, $$

where $A$ and $A_i$ is the sub-watershed and grid cell areas, respectively.

Groundwater exchange

Ponded conditions

Although plausible, TOPMODEL can be allowed to have negative local soil moisture deficits $(\text{i.e., } D_i<0)$, meaning that water has ponded and overland flow is being considered. For the current model however, ponded water and overland flow are being handled by an explicit soil moisture accounting (SMA) scheme and a lateral shallow water movement module, respectively.

Conditions where $D_i<0$ for any grid cell will have its excess water $(x=-D_i)$ added to the SMA system and $D_i$ will be reset to zero. Under these conditions, no recharge will occur at this cell as upward gradients are being assumed. TOPMODEL may continue discharge groundwater to streams (see below).

This exchange, in addition to groundwater discharge to streams, represents the distributed interaction the groundwater system has on the surface. With recharge $(g)$ at the model grid cell computed by the SMA when deficits are present, net basin groundwater exchange $(G)$ is determined by:

$$ G = \sum_i(g-x)_i. $$

Therefore, when $G>0$, the groundwater system is being recharged.

Groundwater discharge to streams

Baseflow

The volumetric flow rate of groundwater discharge to streams $Q_b$ [m³/s] for the entire model domain is given by:

$$ Q_b = \frac{AB}{\Delta t} = \sum_{i=1}^Ml_iq_i, $$

where $B$ is the total groundwater discharge to streams occurring over a time step $\Delta t$, $l_i$ is length of channel in grid cell $i$, here assumed constant and equivalent to the uniform cell width $(w)$ times a sinuosity factor $(\Omega)$, and $M$ is the total number of model cells containing stream channels (termed "stream cells"). Stream cells were identified as cells having a contributing area greater than a set threshold of 1000 cells $\approx$ 2.5km², but could have easily been determined from watercourse mapping.

For every stream cell $i$, groundwater flux to stream cells $b$ [m] during timestep $\Delta t$ is given by:

$$ b_i=\Omega\frac{l_iq_i}{A_i}\Delta t=b_{o,i}\exp\left(\frac{D_\text{inc}-D_i}{m}\right) %\qquad i \in \text{streams} $$

where $b_o$ groundwater flux at stream cell $i$ when the watertable is above the base of the channel, nearly at saturated conditions $(D_\text{inc}-D=0)$ and is defined by:

$$ % b_o=\Omega\cdot \frac{T_o\tan\beta}{w}\Delta t=\Omega\cdot \tan\beta \cdot K_\text{sat}\cdot \Delta t b_o=\Omega\cdot \tan\beta \cdot K_\text{sat}\cdot \Delta t $$

$D_\text{inc}$ is added as an offset, meant to accommodate the degree of channel incision (i.e., the difference between channel thalweg elevation and mean cell elevation).

Finally, basin-wide groundwater discharge to streams

$$ B = \sum_i b_i. $$

Initial conditions

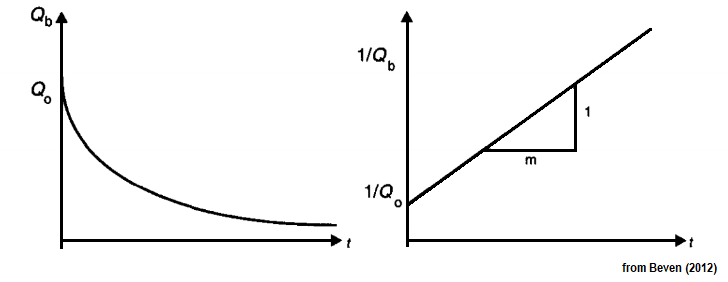
Initial watershed average soil moisture deficit can, in principle, be determined from streamflow records by re-arranging equations in Beven (2012):

$$ %\overline{D}{t=0} = -m \ln\left(\frac{Q{t=0}}{Q_o}\right), %\overline{D}{t=0} = -m\left[\gamma +\ln\left(\frac{Q{t=0}}{\sum_{i=1}^Ml_ia_i}\right)\right], \overline{D}{t=0} = -m\left[\gamma +\ln\left(\frac{Q{t=0}}{A}\right)\right], $$

where $Q_{t=0}$ is the measured stream flow known at the beginning of the model run. The parameter $m$ can be pre-determined from baseflow recession analysis (Beven et.al., 1995; Beven, 2012) and has been incorporated into the ORMGP R-shiny recession analysis tools.

Time stepping

Before every time step, average moisture deficit of every groundwater reservoir is updated at time $t$ by:

$$ \overline{D}t = \frac{1}{A}\sum_i A_i D_i - G{t-1} + B_{t-1} - Q_{t-1}, $$

where $G_{t-1}$ is the total groundwater recharge computed during the previous time step [m], $B_{t-1}$ is the basin-wide (normalized) groundwater discharge to streams, also computed during the previous time step [m], and $Q_{t-1}$ are any additional sources(+)/sinks(-) such as groundwater pumping or exchange between other groundwater reservoirs.

Model-code implementation

It should first be noted that the above formulation is the very similar to the linear decay groundwater storage model, except here, TOPMODEL allows for an approximation of spatial soil moisture distribution, which will, in turn, determine the recharge-runoff distribution that includes groundwater feedback, a mechanism instrumental to integrated groundwater surface water modelling.

Rearranging the above terms gives:

$$ \delta D_i = D_i-\overline{D} = m\left(\gamma - \zeta_i\right) $$

where $\delta D_i$ is the groundwater deficit relative to the regional mean, and is independent of time, and therefore can be parameterized. From this, at any time $t$, the local deficit is thus:

$$ D_{i,t} = \delta D_i + \overline{D}_t $$

Soil Moisture Accounting

The explicit soil moisture accounting (SMA—see Todini and Wallis, 1977; O'Connell, 1991) algorithm used is intentionally simplified. Where this conceptualization differs from typical SMA schemes is that here there is no distinction made among a variety of storage reservoirs commonly conceptualized in established models. For example, all of interception storage, depression storage and soil storage (i.e., soil moisture below field capacity) is assumed representative by a single aggregate store, thus reducing model parameterization. This conceptualization is allowed by the fact that this model is intended for regional-scale application $(\gg1000\text{ km²})$ at a high spatial resolution $(\text{i.e., }50\times 50\text{ m² cells})$. Users must consider the results of the model from a "bird's-eye view," where water retained at surface is indistinguishable from the many stores typically conceptualized in hydrological models. The SMA overall water balance is given as:

$$ \Delta S = P-E-R-G, $$

where $\Delta S$ is the change in (moisture) storage, $P$ is "active" precipitation (which includes direct inputs rainfall $+$ snowmelt and indirect inputs such as runoff originating from upslope areas), which is the source of water to the grid cell. $E$ is total evaporation (transpiration $+$ evaporation from soil and interception stores), $G$ is net groundwater recharge (meaning it accounts for groundwater discharge), $R$ is excess water that is allowed to translate laterally (runoff). All of $E$, $R$, and $G$ are dependent on moisture storage $(S)$ and $S_\text{max}$: the water storage capacity of the grid cell. Both $E$ and $G$ have functional relationships to $S$ and $S_\text{max}$, and are dependent on other variables, whereas $R$ only occurs when there is excess water remaining $(\text{i.e., }S>S_\text{max})$, strictly speaking:

$$ \Delta S = \underbrace{P}{\substack{\text{sources}}} - \underbrace{f\left(E_a,K\text{sat},S,S_\text{max}\right)}{\text{sinks}} - \underbrace{R|{S>S_\text{max}}}_{\text{excess}} $$

Reservoirs

Each model cell consists of a retention reservoir $S_h$ (where water has the potential to drain) and a detention reservoir $S_k$ (where water is held locally but is still considered "mobile" in that if conditions are met, lateral movement would occur); both with a predefined capacity and susceptible to evaporation loss. In addition, any number of cells can be grouped which share a semi-infinite conceptual groundwater store $(S_g)$.

Although conceptual, storage capacities may be related to common hydrological concepts, for instance:

$$ S_h=(\phi-\theta_\text{fc}) z_\text{ext} $$

and

$$ S_k=\theta_\text{fc} z_\text{ext}+F_\text{imp} h_\text{dep}+F_\text{can} h_\text{can}\cdot\text{LAI} $$

where $\phi$ and $\theta_\text{fc}$ are the water contents at saturation (porosity) and field capacity, respectively; $F_\text{imp}$ and $F_\text{can}$ are the fractional cell coverage of impervious area and tree canopy, respectively; $h_\text{dep}$ and $h_\text{can}$ are the capacities of impervious depression and interception stores, respectively; $\text{LAI}$ is the leaf area index and $z_\text{ext}$ is the extinction depth (i.e., the depth of which evaporative loss becomes negligible). Change in detention storage at any time is defined by:

$$ \Delta S_k=k_\text{in}+f_h+b-\left(a_k+f_k+k_\text{out}\right), $$

where $k = q\frac{\Delta t}{w}$ is the volumetric discharge in $(_\text{in})$ and out $(_\text{out})$ of the grid cell and $f_k$ is the volume of mobile storage infiltrating the soil zone; all units are [m]. (Note that groundwater discharge to streams---$b$---only occurs at stream cells and is only a gaining term.) Also note that $k_\text{out}$ only occurs when water stored in $S_k$ exceeds its capacity.

Change in retention storage [m]:

$$ \Delta S_h = y+f_k+x-\left(a_h+f_h+g\right), $$

where $y$ is the atmospheric yield (rainfall + snowmelt), $x$ is groundwater infiltration (i.e., saturation excess) into the soil zone from a high watertable, $a$ is evapotranspiration, and $g$ is groundwater recharge.

And the change in groundwater storage [m] (i.e., net groundwater exchange---positive: recharge; negative: discharge):

$$ \Delta S_g = g-\left(x+b\right). $$

Water balance

The overall water balance, with $a=a_h+a_k$, over each grid cell is then given by:

$$ \Delta S_k+\Delta S_h+\Delta S_g=y+k_\text{in}-\left(a+k_\text{out}\right). $$

Groundwater recharge

Groundwater recharge at cell $i$ is computed as:

$$ g=\min\left(S_h,K_\text{sat}\Delta t\right)+S_k^+\left[1-\exp\left(\frac{-K_\text{sat}}{L}\Delta t\right)\right]. $$

It is important that the second term of the groundwater recharge equation remain to control so-called cascade towers which occur when confluences in the cascade network create unrealistically high stages. (This is mainly a consequence of the simplicity of the overland flow scheme applied here---normally, the pressure term in the shallow water equations provides this control physically.) Here the interface length $L=10\text{ cm}$ globally.

Overland Flow

Laterally moving water leaving the cell $(k_\text{out})$ is corrected (primarily) based on land surface slope and roughness. Water leaving a cell can only be directed to a single cell, but any cell can receive from multiple cells. A "cascade factor", $F_\text{casc}\approx f(\text{slope},\text{roughness},\text{etc.})$, where $0\leq F_\text{casc} \leq 1$, is applied to the current volume stored in the mobile store (in the form of a linear reservoir):

$$ k_\text{out}=F_\text{casc}S_k^+, $$

where $S_k^+>0$ is water in the detention store in excess of the store's capacity. $F_\text{casc}$ is related to land surface gradient by:

$$ F_\text{casc}=1-\exp\left(\frac{\beta^2}{-a}\right), $$

where $\beta$ is land surface gradient and $a$ is a scaling factor (note that the above equation is identical to the Gaussian variogram kernel with a unit range).

References

Ambroise, B., K. Beven, J. Freer, 1996. Toward a generalization of the TOPMODEL concepts: Topographic indices of hydrological similarity, Water Resources Research 32(7): pp.2135—2145.

Beven, K.J., 1986. Hillslope runoff processes and flood frequency characteristics. Hillslope Processes, edited by A.D. Abrahams, Allen and Unwin, Winchester, Mass. pp.187—202.

Beven, K.J., R. Lamb, P.F. Quinn, R. Romanowicz, and J. Freer, 1995. TOPMODEL. In Singh V.P. editor, Computer Models of Watershed Hydrology. Water Resources Publications, Highland Ranch, CO: pp. 627—668.

Beven, K.J. and M.J. Kirkby, 1979. A physically based variable contributing area model of basin hydrology. Hydrological Science Bulletin 24(1):43—69.

Beven, K.J., 2012. Rainfall-Runoff modelling: the primer, 2nd ed. John Wiley & Sons, Ltd. 457pp.