problem497

README

< Previous 　　　　　　　　　　　　　　　　 Next >

497. Random Point in Non-overlapping Rectangles (Medium)

You are given an array of non-overlapping axis-aligned rectangles rects where rects[i] = [ai, bi, xi, yi] indicates that (ai, bi) is the bottom-left corner point of the ith rectangle and (xi, yi) is the top-right corner point of the ith rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.

Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.

Note that an integer point is a point that has integer coordinates.

Implement the Solution class:

• Solution(int[][] rects) Initializes the object with the given rectangles rects.
• int[] pick() Returns a random integer point [u, v] inside the space covered by one of the given rectangles.

 

Example 1:

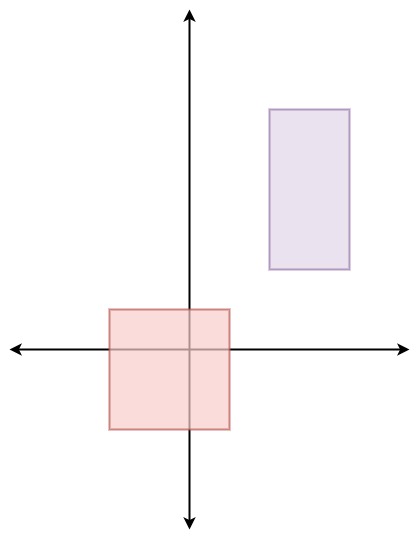
Input
["Solution", "pick", "pick", "pick", "pick", "pick"]
[[[[-2, -2, 1, 1], [2, 2, 4, 6]]], [], [], [], [], []]
Output
[null, [1, -2], [1, -1], [-1, -2], [-2, -2], [0, 0]]
Explanation
Solution solution = new Solution([[-2, -2, 1, 1], [2, 2, 4, 6]]);
solution.pick(); // return [1, -2]
solution.pick(); // return [1, -1]
solution.pick(); // return [-1, -2]
solution.pick(); // return [-2, -2]
solution.pick(); // return [0, 0]

 

Constraints:

• 1 <= rects.length <= 100
• rects[i].length == 4
• -109 <= ai < xi <= 109
• -109 <= bi < yi <= 109
• xi - ai <= 2000
• yi - bi <= 2000
• All the rectangles do not overlap.
• At most 104 calls will be made to pick.

Related Topics

[Reservoir Sampling] [Math] [Binary Search] [Ordered Set] [Prefix Sum] [Randomized]

Similar Questions

1. Random Pick with Weight (Medium)
2. Generate Random Point in a Circle (Medium)