Documentation
¶
Documentation
¶
Overview ¶
Package nvector provides functions for performing geographical position calculations using n-vectors
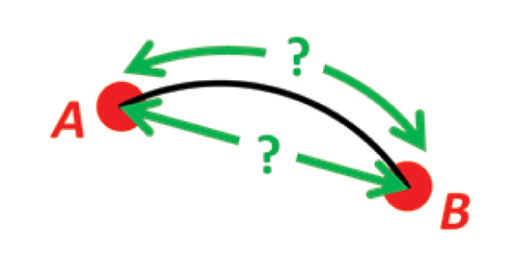
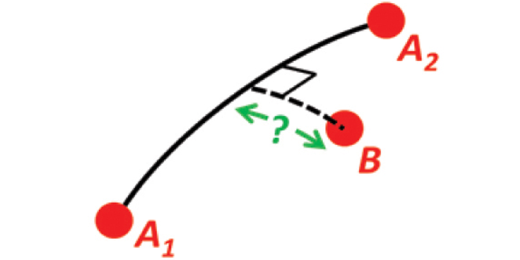
Example (N01AAndBToDelta) ¶
Example 1: A and B to delta
Given two positions A and B. Find the exact vector from A to B in meters north, east and down, and find the direction (azimuth/bearing) to B, relative to north. Use WGS-84 ellipsoid.
See: https://www.ffi.no/en/research/n-vector/#example_1
// PROBLEM:
// Given two positions, A and B as latitudes, longitudes and depths (relative
// to Earth, E):
aLat, aLon, aDepth := 1.0, 2.0, 3.0
bLat, bLon, bDepth := 4.0, 5.0, 6.0
// Find the exact vector between the two positions, given in meters north,
// east, and down, and find the direction (azimuth) to B, relative to north.
//
// Details:
//
// - Assume WGS-84 ellipsoid. The given depths are from the ellipsoid surface.
// - Use position A to define north, east, and down directions. (Due to the
// curvature of Earth and different directions to the North Pole, the north,
// east, and down directions will change (relative to Earth) for different
// places. Position A must be outside the poles for the north and east
// directions to be defined.
// SOLUTION:
// Step 1
//
// First, the given latitudes and longitudes are converted to n-vectors:
a := nvector.Position{
Vector: nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(aLat),
Longitude: nvector.Radians(aLon),
},
nvector.ZAxisNorth,
),
Depth: aDepth,
}
b := nvector.Position{
Vector: nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(bLat),
Longitude: nvector.Radians(bLon),
},
nvector.ZAxisNorth,
),
Depth: bDepth,
}
// Step 2
//
// When the positions are given as n-vectors (and depths), it is easy to find
// the delta vector decomposed in E. No ellipsoid is specified when calling
// the function, thus WGS-84 (default) is used:
abE := nvector.Delta(a, b, nvector.WGS84, nvector.ZAxisNorth)
// Step 3
//
// We now have the delta vector from A to B, but the three coordinates of the
// vector are along the Earth coordinate frame E, while we need the
// coordinates to be north, east and down. To get this, we define a
// North-East-Down coordinate frame called N, and then we need the rotation
// matrix (direction cosine matrix) rEN to go between E and N. We have a
// simple function that calculates rEN from an n-vector, and we use this
// function (using the n-vector at position A):
rEN := nvector.ToRotationMatrix(a.Vector, nvector.ZAxisNorth)
// Step 4
//
// Now the delta vector is easily decomposed in N. Since the vector is
// decomposed in E, we must use rNE (rNE is the transpose of rEN):
abN := abE.Transform(rEN.Transpose())
// Step 5
//
// The three components of abN are the north, east and down displacements from
// A to B in meters. The azimuth is simply found from element 1 and 2 of the
// vector (the north and east components):
azimuth := math.Atan2(abN.Y, abN.X)
fmt.Printf("Delta north, east, down = %.8f, %.8f, %.8f m\n", abN.X, abN.Y, abN.Z)
fmt.Printf("Azimuth = %.8f deg\n", nvector.Degrees(azimuth))
Output: Delta north, east, down = 331730.23478089, 332997.87498927, 17404.27136194 m Azimuth = 45.10926324 deg
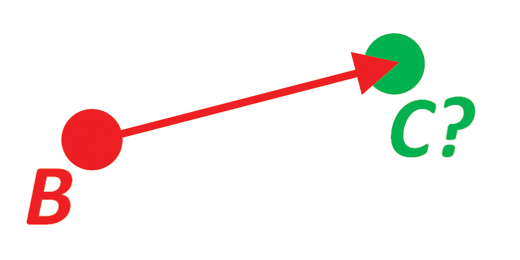
Example (N02BAndDeltaToC) ¶
Example 2: B and delta to C
Given the position of vehicle B and a bearing and distance to an object C. Find the exact position of C. Use WGS-72 ellipsoid.
See: https://www.ffi.no/en/research/n-vector/#example_2
// PROBLEM:
// A radar or sonar attached to a vehicle B (Body coordinate frame) measures
// the distance and direction to an object C. We assume that the distance and
// two angles measured by the sensor (typically bearing and elevation relative
// to B) are already converted (by converting from spherical to Cartesian
// coordinates) to the vector bcB (i.e. the vector from B to C, decomposed in
// B):
bcB := nvector.Vector{X: 3000, Y: 2000, Z: 100}
// The position of B is given as an n-vector and a depth:
b := nvector.Position{
Vector: nvector.Vector{X: 1, Y: 2, Z: 3}.Normalize(),
Depth: -400.0,
}
// The orientation (attitude) of B is given as rNB, specified as yaw, pitch,
// roll:
rNB := nvector.EulerZYXToRotationMatrix(nvector.EulerZYX{
Z: nvector.Radians(10),
Y: nvector.Radians(20),
X: nvector.Radians(30),
})
// Use the WGS-72 ellipsoid:
e := nvector.WGS72
// Find the exact position of object C as an n-vector and a depth.
// SOLUTION:
// Step 1
//
// The delta vector is given in B. It should be decomposed in E before using
// it, and thus we need rEB. This matrix is found from the matrices rEN and
// rNB, and we need to find rEN, as in Example 1:
rEN := nvector.ToRotationMatrix(b.Vector, nvector.ZAxisNorth)
// Step 2
//
// Now, we can find rEB y using that the closest frames cancel when
// multiplying two rotation matrices (i.e. N is cancelled here):
rEB := rEN.Multiply(rNB)
// Step 3
//
// The delta vector is now decomposed in E:
bcE := bcB.Transform(rEB)
// Step 4
//
// It is now easy to find the position of C using destination (with custom
// ellipsoid overriding the default WGS-84):
c := nvector.Destination(b, bcE, e, nvector.ZAxisNorth)
// Use human-friendly outputs:
gc := nvector.ToGeodeticCoordinates(c.Vector, nvector.ZAxisNorth)
h := -c.Depth
fmt.Printf(
"Pos C: lat, lon = %.8f, %.8f deg, height = %.8f m\n",
nvector.Degrees(gc.Latitude),
nvector.Degrees(gc.Longitude),
h,
)
Output: Pos C: lat, lon = 53.32637826, 63.46812344 deg, height = 406.00719607 m
Example (N03ECEFToLatLon) ¶
Example 3: ECEF-vector to geodetic latitude
Given an ECEF-vector of a position. Find geodetic latitude, longitude and height (using WGS-84 ellipsoid).
See: https://www.ffi.no/en/research/n-vector/#example_3
// PROBLEM:
// Position B is given as an “ECEF-vector” pb (i.e. a vector from E, the
// center of the Earth, to B, decomposed in E):
pb := nvector.Vector{X: 0.71, Y: -0.72, Z: 0.1}.Scale(6371e3)
// Find the geodetic latitude, longitude and height, assuming WGS-84
// ellipsoid.
// SOLUTION:
// Step 1
//
// We have a function that converts ECEF-vectors to n-vectors:
b := nvector.FromECEF(pb, nvector.WGS84, nvector.ZAxisNorth)
// Step 2
//
// Find latitude, longitude and height:
gc := nvector.ToGeodeticCoordinates(b.Vector, nvector.ZAxisNorth)
h := -b.Depth
fmt.Printf(
"Pos B: lat, lon = %.8f, %.8f deg, height = %.8f m\n",
nvector.Degrees(gc.Latitude),
nvector.Degrees(gc.Longitude),
h,
)
Output: Pos B: lat, lon = 5.68507573, -45.40066326 deg, height = 95772.10761822 m
Example (N04LatLonToECEF) ¶
Example 4: Geodetic latitude to ECEF-vector
Given geodetic latitude, longitude and height. Find the ECEF-vector (using WGS-84 ellipsoid).
See: https://www.ffi.no/en/research/n-vector/#example_4
// PROBLEM:
// Geodetic latitude, longitude and height are given for position B:
bLat, bLon, bHeight := 1.0, 2.0, 3.0
// Find the ECEF-vector for this position.
// SOLUTION:
// Step 1: First, the given latitude and longitude are converted to n-vector:
b := nvector.Position{
Vector: nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(bLat),
Longitude: nvector.Radians(bLon),
},
nvector.ZAxisNorth,
),
Depth: -bHeight,
}
// Step 2: Convert to an ECEF-vector:
pb := nvector.ToECEF(b, nvector.WGS84, nvector.ZAxisNorth)
fmt.Printf("p_EB_E = [%.8f, %.8f, %.8f] m\n", pb.X, pb.Y, pb.Z)
Output: p_EB_E = [6373290.27721828, 222560.20067474, 110568.82718179] m
Example (N05SurfaceDistance) ¶
Example 5: Surface distance
Given position A and B. Find the surface distance (i.e. great circle distance) and the Euclidean distance.
See: https://www.ffi.no/en/research/n-vector/#example_5
// PROBLEM:
// Given two positions A and B as n-vectors:
a := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(88),
Longitude: nvector.Radians(0),
},
nvector.ZAxisNorth,
)
b := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(89),
Longitude: nvector.Radians(-170),
},
nvector.ZAxisNorth,
)
// Find the surface distance (i.e. great circle distance). The heights of A
// and B are not relevant (i.e. if they do not have zero height, we seek the
// distance between the points that are at the surface of the Earth, directly
// above/below A and B). The Euclidean distance (chord length) should also be
// found.
// Use Earth radius r:
r := 6371e3
// SOLUTION:
// Find the great circle distance:
gcd := math.Atan2(a.Cross(b).Norm(), a.Dot(b)) * r
// Find the Euclidean distance:
ed := b.Sub(a).Norm() * r
fmt.Printf(
"Great circle distance = %.8f m, Euclidean distance = %.8f m\n",
gcd,
ed,
)
Output: Great circle distance = 332456.44410534 m, Euclidean distance = 332418.72485681 m
Example (N06InterpolatedPosition) ¶
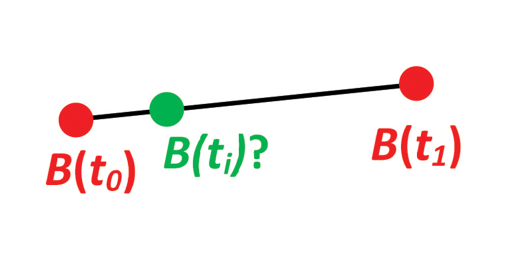
Example 6: Interpolated position
Given the position of B at time t(0) and t(1). Find an interpolated position at time t(i).
See: https://www.ffi.no/en/research/n-vector/#example_6
// PROBLEM:
// Given the position of B at time t0 and t1, pt0 and pt1:
t0, t1, ti := 10.0, 20.0, 16.0
pt0 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(89.9),
Longitude: nvector.Radians(-150),
},
nvector.ZAxisNorth,
)
pt1 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(89.9),
Longitude: nvector.Radians(150),
},
nvector.ZAxisNorth,
)
// Find an interpolated position at time ti, pti. All positions are given as
// n-vectors.
// SOLUTION:
// Standard interpolation can be used directly with n-vectors:
pti := pt0.Add(pt1.Sub(pt0).Scale((ti - t0) / (t1 - t0)))
// Use human-friendly outputs:
gc := nvector.ToGeodeticCoordinates(pti, nvector.ZAxisNorth)
fmt.Printf(
"Interpolated position: lat, lon = %.8f, %.8f deg\n",
nvector.Degrees(gc.Latitude),
nvector.Degrees(gc.Longitude),
)
Output: Interpolated position: lat, lon = 89.91282200, 173.41322445 deg
Example (N07MeanPosition) ¶
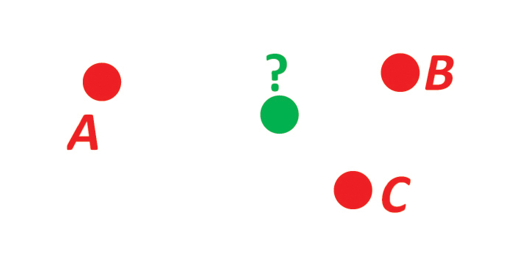
Example 7: Mean position/center
Given three positions A, B, and C. Find the mean position (center/midpoint).
See: https://www.ffi.no/en/research/n-vector/#example_7
// PROBLEM:
// Three positions A, B, and C are given as n-vectors:
a := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(90),
Longitude: nvector.Radians(0),
},
nvector.ZAxisNorth,
)
b := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(60),
Longitude: nvector.Radians(10),
},
nvector.ZAxisNorth,
)
c := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(50),
Longitude: nvector.Radians(-20),
},
nvector.ZAxisNorth,
)
// Find the mean position, M. Note that the calculation is independent of the
// heights/depths of the positions.
// SOLUTION:
// The mean position is simply given by the mean n-vector:
m := a.Add(b).Add(c).Normalize()
fmt.Printf("Mean position: [%.8f, %.8f, %.8f]\n", m.X, m.Y, m.Z)
Output: Mean position: [0.38411717, -0.04660241, 0.92210749]
Example (N08AAndDistanceToB) ¶
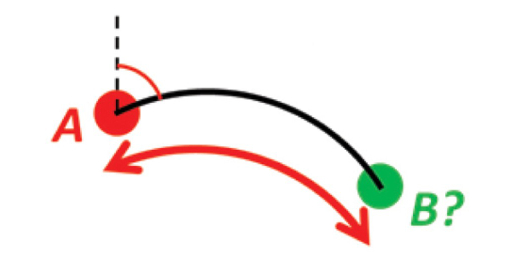
Example 8: A and azimuth/distance to B
Given position A and an azimuth/bearing and a (great circle) distance. Find the destination point B.
See: https://www.ffi.no/en/research/n-vector/#example_8
// PROBLEM:
// Position A is given as n-vector:
a := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(80),
Longitude: nvector.Radians(-90),
},
nvector.ZAxisNorth,
)
// We also have an initial direction of travel given as an azimuth (bearing)
// relative to north (clockwise), and finally the distance to travel along a
// great circle is given:
azimuth := nvector.Radians(200)
gcd := 1000.0
// Use Earth radius r:
r := 6371e3
// Find the destination point B.
//
// In geodesy, this is known as "The first geodetic problem" or "The direct
// geodetic problem" for a sphere, and we see that this is similar to Example
// 2, but now the delta is given as an azimuth and a great circle distance.
// "The second/inverse geodetic problem" for a sphere is already solved in
// Examples 1 and 5.
// SOLUTION:
// The azimuth (relative to north) is a singular quantity (undefined at the
// Poles), but from this angle we can find a (non-singular) quantity that is
// more convenient when working with vector algebra: a vector d that points in
// the initial direction. We find this from azimuth by first finding the north
// and east vectors at the start point, with unit lengths.
//
// Here we have assumed that our coordinate frame E has its z-axis along the
// rotational axis of the Earth, pointing towards the North Pole. Hence, this
// axis is given by [1, 0, 0]:
e := nvector.Vector{X: 1, Y: 0, Z: 0}.
Transform(nvector.ZAxisNorth.Transpose()).
Cross(a).
Normalize()
n := a.Cross(e)
// The two vectors n and e are horizontal, orthogonal, and span the tangent
// plane at the initial position. A unit vector d in the direction of the
// azimuth is now given by:
d := n.Scale(math.Cos(azimuth)).Add(e.Scale(math.Sin(azimuth)))
// With the initial direction given as d instead of azimuth, it is now quite
// simple to find b. We know that d and a are orthogonal, and they will span
// the plane where b will lie. Thus, we can use sin and cos in the same manner
// as above, with the angle traveled given by gcd / r:
b := a.Scale(math.Cos(gcd / r)).Add(d.Scale(math.Sin(gcd / r)))
// Use human-friendly outputs:
gc := nvector.ToGeodeticCoordinates(b, nvector.ZAxisNorth)
fmt.Printf(
"Destination: lat, lon = %.8f, %.8f deg\n",
nvector.Degrees(gc.Latitude),
nvector.Degrees(gc.Longitude),
)
Output: Destination: lat, lon = 79.99154867, -90.01769837 deg
Example (N09IntersectionOfPaths) ¶
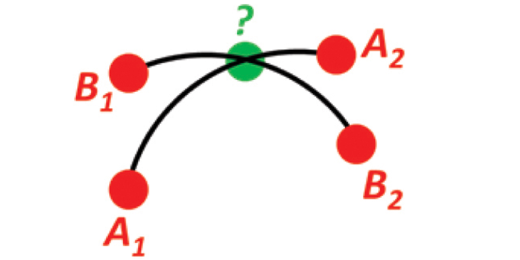
Example 9: Intersection of two paths
Given path A going through A(1) and A(2), and path B going through B(1) and B(2). Find the intersection of the two paths.
See: https://www.ffi.no/en/research/n-vector/#example_9
// PROBLEM:
// Define a path from two given positions (at the surface of a spherical
// Earth), as the great circle that goes through the two points (assuming that
// the two positions are not antipodal).
// Path A is given by a1 and a2:
a1 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(50),
Longitude: nvector.Radians(180),
},
nvector.ZAxisNorth,
)
a2 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(90),
Longitude: nvector.Radians(180),
},
nvector.ZAxisNorth,
)
// While path B is given by b1 and b2:
b1 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(60),
Longitude: nvector.Radians(160),
},
nvector.ZAxisNorth,
)
b2 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(80),
Longitude: nvector.Radians(-140),
},
nvector.ZAxisNorth,
)
// Find the position C where the two paths intersect.
// SOLUTION:
// A convenient way to represent a great circle is by its normal vector (i.e.
// the normal vector to the plane containing the great circle). This normal
// vector is simply found by taking the cross product of the two n-vectors
// defining the great circle (path). Having the normal vectors to both paths,
// the intersection is now simply found by taking the cross product of the two
// normal vectors:
cTmp := a1.Cross(a2).Cross(b1.Cross(b2))
// Note that there will be two places where the great circles intersect, and
// thus two solutions are found. Selecting the solution that is closest to
// e.g. a1 can be achieved by selecting the solution that has a positive dot
// product with a1 (or the mean position from Example 7 could be used instead
// of a1):
c := cTmp.Scale(math.Copysign(1, cTmp.Dot(a1)))
// Use human-friendly outputs:
gc := nvector.ToGeodeticCoordinates(c, nvector.ZAxisNorth)
fmt.Printf(
"Intersection: lat, lon = %.8f, %.8f deg\n",
nvector.Degrees(gc.Latitude),
nvector.Degrees(gc.Longitude),
)
Output: Intersection: lat, lon = 74.16344802, 180.00000000 deg
Example (N10CrossTrackDistance) ¶
Example 10: Cross track distance (cross track error)
Given path A going through A(1) and A(2), and a point B. Find the cross track distance/cross track error between B and the path.
See https://www.ffi.no/en/research/n-vector/#example_10
// PROBLEM:
// Path A is given by the two n-vectors a1 and a2 (as in the previous
// example):
a1 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(0),
Longitude: nvector.Radians(0),
},
nvector.ZAxisNorth,
)
a2 := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(10),
Longitude: nvector.Radians(0),
},
nvector.ZAxisNorth,
)
// And a position B is given by b:
b := nvector.FromGeodeticCoordinates(
nvector.GeodeticCoordinates{
Latitude: nvector.Radians(1),
Longitude: nvector.Radians(0.1),
},
nvector.ZAxisNorth,
)
// Find the cross track distance between the path A (i.e. the great circle
// through a1 and a2) and the position B (i.e. the shortest distance at the
// surface, between the great circle and B). Also, find the Euclidean distance
// between B and the plane defined by the great circle.
// Use Earth radius r:
r := 6371e3
// SOLUTION:
// First, find the normal to the great circle, with direction given by the
// right hand rule and the direction of travel:
c := a1.Cross(a2).Normalize()
// Find the great circle cross track distance:
gcd := -math.Asin(c.Dot(b)) * r
// Finding the Euclidean distance is even simpler, since it is the projection
// of b onto c, thus simply the dot product:
ed := -c.Dot(b) * r
// For both gcd and ed, positive answers means that B is to the right of the
// track.
fmt.Printf("Cross track distance = %.8f m, Euclidean = %.8f m\n", gcd, ed)
Output: Cross track distance = 11117.79911015 m, Euclidean = 11117.79346741 m
Index ¶
Examples ¶
Constants ¶
This section is empty.
Variables ¶
var ( // ZAxisNorth defines the axes of the coordinate frame E (Earth-Centred, // Earth-Fixed, ECEF) when the z-axis points to the North Pole. // // The z-axis points to the North Pole and x-axis points to the point where // latitude = longitude = 0. This choice is very common in many fields. // // See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/R_Ee.m#L48 ZAxisNorth = Matrix{ 0, 0, 1, 0, 1, 0, -1, 0, 0, } // XAxisNorth defines the axes of the coordinate frame E (Earth-Centred, // Earth-Fixed, ECEF) when the x-axis points to the North Pole. // // The x-axis points to the North Pole, y-axis points towards longitude +90deg // (east) and latitude = 0. This choice of axis directions ensures that at // zero latitude and longitude, N (North-East-Down) has the same orientation // as E. If roll/pitch/yaw are zero, also B (Body, forward, starboard, down) // has this orientation. In this manner, the axes of E is chosen to correspond // with the axes of N and B. // // See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/R_Ee.m#L55 XAxisNorth = Matrix{ 1, 0, 0, 0, 1, 0, 0, 0, 1, } )
var ( // GRS80 is the Geodetic Reference System 1980 ellipsoid. // // See: https://github.com/chrisveness/geodesy/blob/761587cd748bd9f7c9825195eba4a9fc5891b859/latlon-ellipsoidal-datum.js#L45 GRS80 = Ellipsoid{6378137, 6356752.314140356, 1 / 298.257222101} // WGS72 is the World Geodetic System 1972 ellipsoid. // // See: https://github.com/chrisveness/geodesy/blob/761587cd748bd9f7c9825195eba4a9fc5891b859/latlon-ellipsoidal-datum.js#L47 WGS72 = Ellipsoid{6378135, 6356750.520016094, 1 / 298.26} // WGS84 is the World Geodetic System 1984 ellipsoid. // // See: https://github.com/chrisveness/geodesy/blob/761587cd748bd9f7c9825195eba4a9fc5891b859/latlon-ellipsoidal-datum.js#L39 WGS84 = Ellipsoid{6378137, 6356752.314245179, 1 / 298.257223563} )
Functions ¶
Types ¶
type EulerXYZ ¶
type EulerXYZ struct {
X, Y, Z float64
}
EulerXYZ is a set of Euler angles in XYZ order.
func RotationMatrixToEulerXYZ ¶
RotationMatrixToEulerXYZ converts a rotation matrix to Euler angles in XYZ order.
See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/R2xyz.m
type EulerZYX ¶
type EulerZYX struct {
Z, Y, X float64
}
EulerZYX is a set of Euler angles in ZYX order.
func RotationMatrixToEulerZYX ¶
RotationMatrixToEulerZYX converts a rotation matrix to Euler angles in ZYX order.
See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/R2zyx.m
type GeodeticCoordinates ¶
type GeodeticCoordinates struct {
Latitude, Longitude float64
}
GeodeticCoordinates is a geodetic latitude and longitude.
Latitude and Longitude are given in radians.
func ToGeodeticCoordinates ¶
func ToGeodeticCoordinates(v Vector, f Matrix) GeodeticCoordinates
ToGeodeticCoordinates converts an n-vector to geodetic coordinates.
f is the coordinate frame in which the n-vector is decomposed.
type Matrix ¶
Matrix is a 3x3 matrix.
func EulerXYZToRotationMatrix ¶
EulerXYZToRotationMatrix converts Euler angles in XYZ order to a rotation matrix.
See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/xyz2R.m
func EulerZYXToRotationMatrix ¶
EulerZYXToRotationMatrix converts Euler angles in ZYX order to a rotation matrix.
See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/zyx2R.m
func ToRotationMatrix ¶
ToRotationMatrix converts n-vector to a rotation matrix.
f is the coordinate frame in which the n-vector is decomposed.
See: https://github.com/FFI-no/n-vector/blob/82d749a67cc9f332f48c51aa969cdc277b4199f2/nvector/n_E2R_EN.m
func ToRotationMatrixUsingWanderAzimuth ¶
ToRotationMatrixUsingWanderAzimuth converts an n-vector and a wander azimuth angle to a rotation matrix.
w is the wander azimuth angle in radians. f is the coordinate frame in which the n-vector is decomposed.
type Position ¶
type Position struct {
// Vector is the n-vector.
Vector Vector
// Depth is the depth in meters below the ellipsoid.
Depth float64
}
Position is an n-vector with an associated depth. Together, they represent a concrete position relative to the ellipsoid, similar to an ECEF position vector.
func Destination ¶
Destination finds a n-vector from a reference n-vector position, and a delta ECEF position vector.
f is the coordinate frame in which the vectors are decomposed.
type Vector ¶
type Vector struct {
X, Y, Z float64
}
Vector is a 3D vector.
func Delta ¶
Delta finds a delta ECEF position vector from a reference n-vector position, and a target n-vector position.
f is the coordinate frame in which the vectors are decomposed.
func FromGeodeticCoordinates ¶
func FromGeodeticCoordinates(c GeodeticCoordinates, f Matrix) Vector
FromGeodeticCoordinates converts geodetic coordinates to an n-vector.
f is the coordinate frame in which the n-vector is decomposed.
func FromRotationMatrix ¶
FromRotationMatrix converts a rotation matrix to an n-vector.
See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/R_EL2n_E.m See: https://github.com/FFI-no/n-vector/blob/f77f43d18ddb6b8ea4e1a8bb23a53700af965abb/nvector/R_EN2n_E.m
func ToECEF ¶
ToECEF converts an n-vector and depth to an ECEF position vector.
f is the coordinate frame in which the vectors are decomposed.