0291

README

291. 蒙德里安的梦想

题目

求把 $N \times M$ 的棋盘分割成若干个 $1 \times 2$ 的的长方形，有多少种方案。

例如当 $N=2，M=4$ 时，共有 $5$ 种方案。当 $N=2，M=3$ 时，共有 $3$ 种方案。

如下图所示：

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 $N$ 和 $M$。

当输入用例 $N=0，M=0$ 时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

数据范围

$1 \le N,M \le 11$

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

题解

前置题目：0338

前置知识：简单数论

本题知识：动态规划-状态压缩DP

题目分析

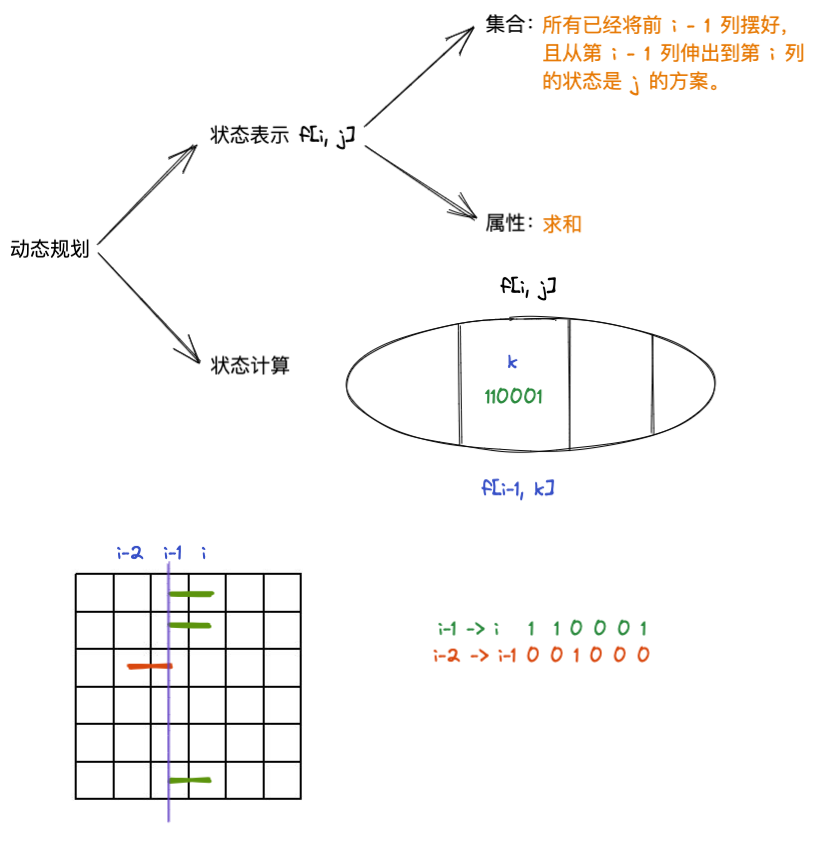
八字箴言：化零为整，化整为零（即状态表示，状态计算）

长方形的摆法有两种，横着摆和竖着摆，所有长方形合在一起还原整个棋盘 所以可以先只横着摆，然后校验剩余的地方是否可以合法竖着摆

如图所示，是一种前 i - 1 列摆好，第 i - 1列伸出到第 i 列的状态是 110001 的方案，设为 f[i, 110001] 这种方案的值又是由前 i - 2 列摆好，第 i -2 列伸出到第 i - 1列的各种合法状态的数量之和

那么怎么样的状态是合法的呢？

1. 两种状态不能冲突
2. 空下的方格可以完美的竖着摆放

初始化 f[0, 0] = 1，前 -1 列已经摆好，且 -1 列伸出到 0列的状态是 000000，这种方案只有 1 种：空棋盘。 最终答案 f[m, 0]，棋盘列数是 0 ~ m - 1，所以 f[m, 0] 根据定义就是刚好将棋盘摆满

复杂度

时间复杂度 = 状态数量 x 转移计算量 = 11*2^11 x 2^11 ≈ 4*10^7

实现细节

预处理：

• 将如图 i - 1 列的所有合法情况事先计算出来
• 在任何一种给定的 i - 1到 i 的状态下，从第 i - 2 到第 i - 1 的合法状态事先计算出来