algorithms

README

Search in a Binary Search Tree

Problem

Given the root node of a binary search tree (BST) and an integer val, return the node in the BST that the node's value equals val. If such a node does not exist, return null.

Examples

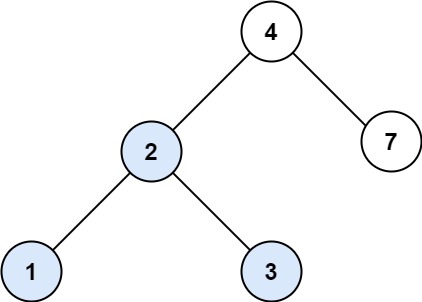
Input: root = [4,2,7,1,3], val = 2

Output: [2,1,3]

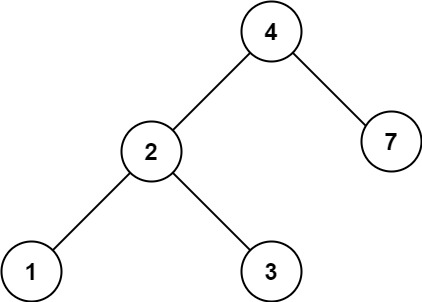
Input: root = [4,2,7,1,3], val = 5

Output: []

Solution

Recursive Solution

The recursive solution is pretty straightforward. If the current node is nil, we return nil. If the current node's value is equal to val, we return the current node. Otherwise, we check if the value is less than the current node's value and search the left subtree. Otherwise, we search the right subtree.

Code

Go

func SearchBST(root *TreeNode, val int) *TreeNode {
    if root == nil {
        return nil
    }

    if val == root.Val {
        return root
    } else {
        if val > root.Val {
            return SearchBST(root.Right, val)
        } else {
            return SearchBST(root.Left, val)
        }
    }
}

Complexity Analysis

• Time Complexity : O(n), where n is the number of nodes in the tree. In the worst case, we might have to visit all nodes of the BST.

• Space Complexity : O(n). The number of recursive calls is bound by the height of the tree. In the worst case, the tree is linear and the height is in O(n). Therefore, space complexity due to recursive calls on the stack is O(n) in the worst case.

Documentation

Index

• type TreeNode
  • func SearchBST(root *TreeNode, val int) *TreeNode

Types

type TreeNode

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

Definition for a binary tree node

func SearchBST

func SearchBST(root *TreeNode, val int) *TreeNode

Recursive solution