maxProfit

README

Given

Click here for official problem page.

You are given an array prices where prices[i] is the price of a given stock on the ith day.

You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return $0$.

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Example 2:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

Constraints:

• $1 <=$ prices.length $<= 10^5$
• $0 <=$ prices[i] $<= 10^4$

Solutions

We need to find out the maximum difference (which will be the maximum profit) between two numbers in the given array. Also, the second number (selling price) must be larger than the first one (buying price).

In formal terms, we need to find max(prices[j] - prices[i]) for every $i$ and $j$ such at $j > i$

Approach I

Complexity Analysis:

• Time complexity: $O(n^2)$. Loop runs $n(n-1)/2$ times
• Space complexity: $O(1)$

Golang solution

func maxProfit(prices []int) int{
    var max_profit int = 0
    var profit int
    for i := 0; i < len(prices) - 1; i++ {
        for j := i+1; j < len(prices); j++ {
            profit = prices[j] - prices[i]
            if profit > max_profit {
                max_profit = profit
            }
        }
    }
    return max_profit
}

Python solution

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        max_profit = 0
        for i in range(len(prices) - 1):
            for j in range(i + 1, len(prices)):
                profit = prices[j] - prices[i]
                if profit > max_profit:
                    max_profit = profit
                    
        return max_profit

Approach II

Algorithm

Say the given array is:

[7, 1, 5, 3, 6, 4]

If we plot the numbers of the given array on a graph, we get:

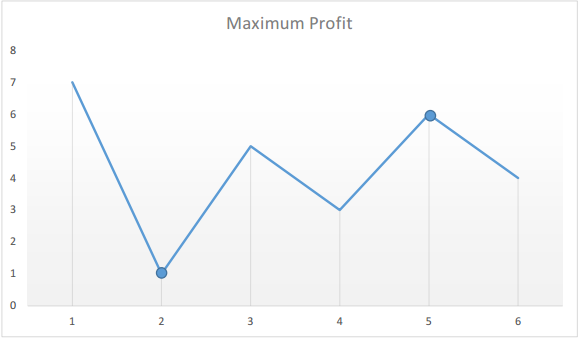
The points of interest are the peaks and valleys in the given graph. We need to find the largest peak following the smallest valley. We can maintain two variables - minprice and maxprofit corresponding to the smallest valley and maximum profit (maximum difference between selling price and minprice) obtained so far respectively.

Complexity Analysis

• Time Complexity: $O(n)$
• Space Complexity: $O(1)$

Python solution

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        min_price = float('inf')
        max_profit = 0
        for i in range(len(prices)):
            if prices[i] < min_price:
                min_price = prices[i]
            elif prices[i] - min_price > max_profit:
                max_profit = prices[i] - min_price
                
        return max_profit

Golang solution

func maxProfit(prices []int) int {
    min_price := 9223372036854775807 // maximum value of int64
    max_profit := 0
    for i := 0; i < len(prices); i++ {
        if prices[i] < min_price{
            min_price = prices[i]
        }
        if prices[i] - min_price > max_profit {
            max_profit = prices[i] - min_price
        }
    }
    return max_profit
}

---