linked_list_cycle_ii

README

142. Linked List Cycle II

Level: Medium

https://leetcode.com/problems/linked-list-cycle-ii/

---

Description

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle.

Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

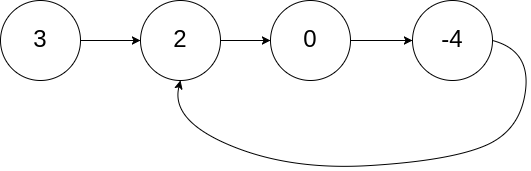
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

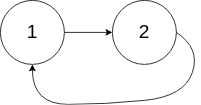
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 104]

-105 <= Node.val <= 105`

pos is -1 or a valid index in the linked-list.

---

Solution

Intuition

When tackling this problem, the first thought that comes to mind is the classic "hare and tortoise" algorithm, also known as Floyd's cycle detection algorithm. It uses two pointers moving at different speeds to determine whether a cycle exists in a linked list. If a cycle exists, the pointers will eventually meet.

Approach

Our approach is to use Floyd's cycle detection algorithm. We start with two pointers, slow and fast, both initialized at the head of the list. The slow pointer moves one step at a time, while the fast pointer moves two steps at a time. If there's a cycle in the list, these two pointers will eventually meet.

When the two pointers meet, we reset the slow pointer to the head of the list and then move both pointers one step at a time. The point where they meet again is the beginning of the cycle.

If the fast pointer reaches the end of the list, it means there's no cycle, and we return null.

Complexity

• Time complexity: The time complexity is O(n), where n is the number of nodes in the list. In the worst-case scenario, we have to traverse the entire list once.

• Space complexity: The space complexity is O(1). No matter the size of the linked list, we only use two pointers, so the space usage is constant.

---

Code

Here are the solution and test files:

• Solution Code
• Test Code

Documentation

Index

• type ListNode

Types

type ListNode

type ListNode struct {
	Val  int
	Next *ListNode
}